使用波束包络法分析大型光学问题
除了传统的数值方法以外,“波动光学模块”还提供专用的波束包络方法,用于模拟大型光学器件。相比传统方法,波束包络法可以大幅节省计算资源,广泛应用于定向耦合器、光纤布拉格光栅、透镜系统、波导、外部光学系统、光纤耦合、激光二极管堆,以及激光束传输系统等。
波束包络法是一种先进的数值方法,能够在不依赖近似方法的情况下,分析大型光学问题仿真中缓慢变化的电场包络。与传统方法相比,这种方法在求解各个波的传播时所需的网格单元数要少得多。
深入分析微纳光学器件
“波动光学模块”是 COMSOL Multiphysics® 的附加产品,主要用于帮助工程师和科研人员深入理解、预测和研究电磁波在光学应用中的传播和谐振效应。通过分析电磁场分布、透射和反射系数以及功率损耗等参数,为产品设计和优化提供更加精准、高效的方案。
对于实际工作场景中的光子器件、集成光路、光波导、耦合器、光纤等,常常需要考虑多个物理效应的影响。软件提供的多物理场耦合功能,方便您在同一个软件环境中耦合如应力-光、电-光、声-光及电磁热等多物理场效应,更准确的分析真实场景下的光学问题。
联系 COMSOL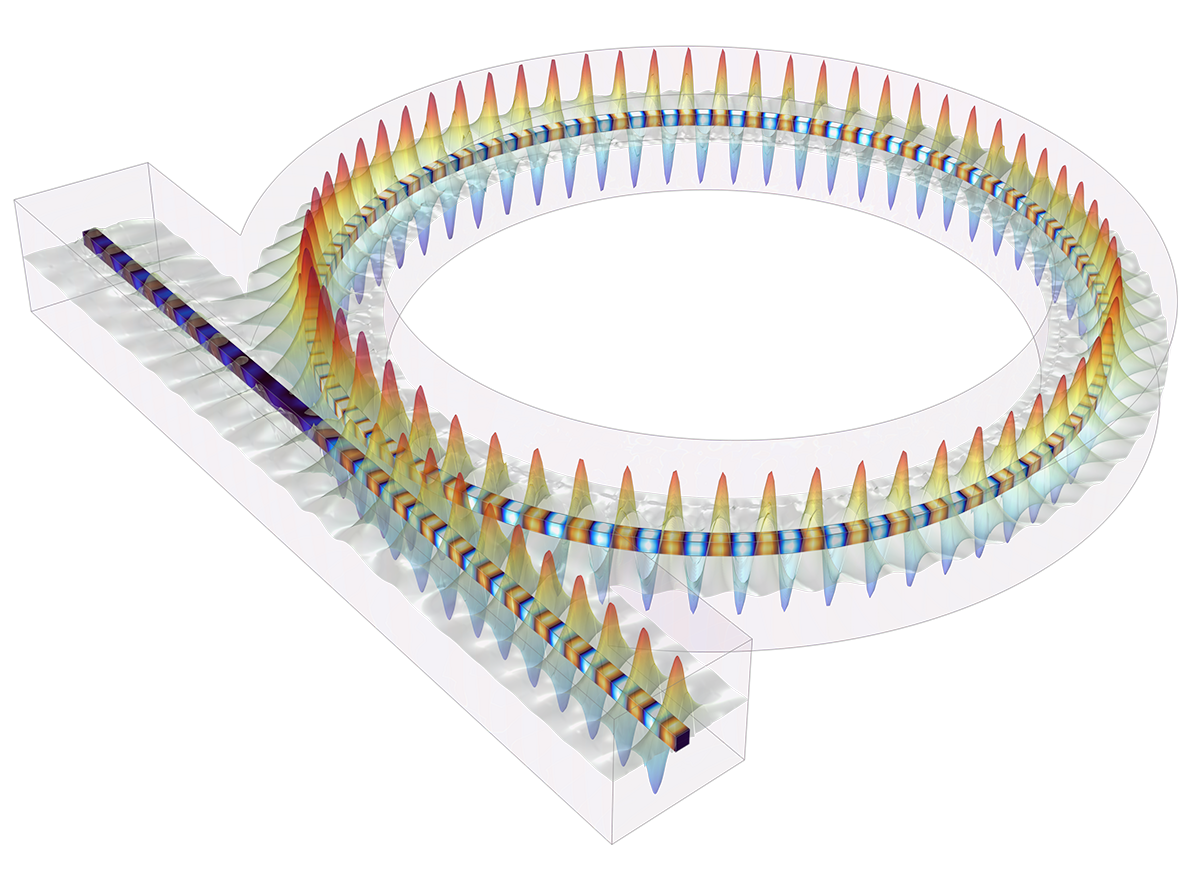
除了传统的数值方法以外,“波动光学模块”还提供专用的波束包络方法,用于模拟大型光学器件。相比传统方法,波束包络法可以大幅节省计算资源,广泛应用于定向耦合器、光纤布拉格光栅、透镜系统、波导、外部光学系统、光纤耦合、激光二极管堆,以及激光束传输系统等。
波束包络法是一种先进的数值方法,能够在不依赖近似方法的情况下,分析大型光学问题仿真中缓慢变化的电场包络。与传统方法相比,这种方法在求解各个波的传播时所需的网格单元数要少得多。
使用 COMSOL® 软件分析各种光学系统

光纤中的模态分析和波的传播。
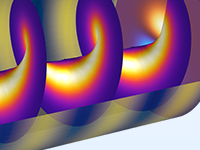
高斯波或平面波在电介质或自由空间中的传播。

计算波导的透射和反射系数。

分析近距离波导之间的物理场耦合。

平面波和高斯光束的散射。

表面等离激元和等离极化激元的电磁激励。

光子晶体和带隙结构。

二次谐波产生、自聚焦效应和其他非线性效应。

激光腔的谐振频率和阈值增益。

光栅、超材料和一般周期性结构的透射、反射和衍射。
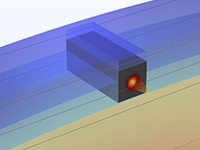
波导中应力诱导的双折射效应。
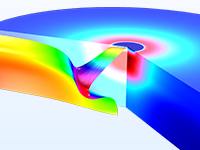
光电器件中的发射、吸收和折射率的变化情况。
阅读以下内容,了解“波动光学模块”的功能
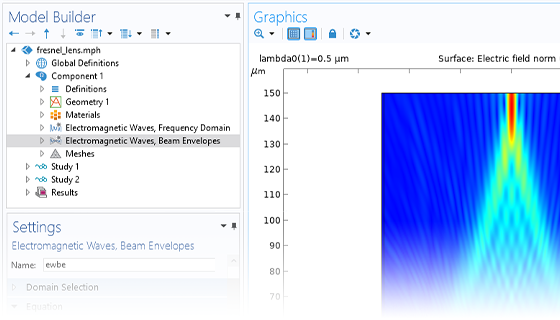
“波动光学模块”可以帮助用户轻松地在二维、二维轴对称和三维几何空间中快速建立模型,仿真工作流程简单明了,一般包括:创建或导入几何、选择材料、选择合适的波动光学 接口、定义边界条件和初始条件、定义网格、选择求解器以及将结果可视化,所有这些步骤都可以在 COMSOL Multiphysics® 环境中执行。软件预置了相应的网格划分和求解器设置,并支持手动修改这些设置。
“波动光学模块”基于麦克斯韦方程和光在不同介质中传播的材料定律,来计算电磁场和波的传播,分析光学器件中的光传播。
“波动光学模块”支持频域和时域建模,包括特征频率和模式分析。
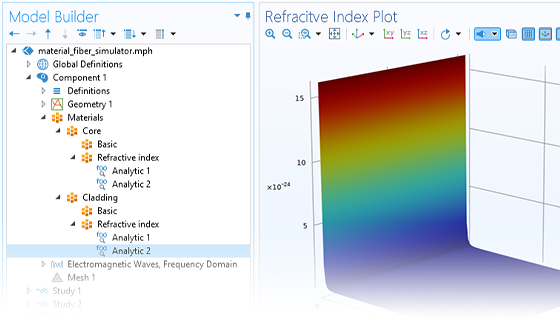
“波动光学模块”提供了内置的光学材料库,方便用户选择,也支持用户自定义光学材料:可以指定相对介电常数或折射率,也可以包含更高级的材料属性,如 Debye、Drude-Lorentz 和 Sellmeier 色散等;还支持各向异性材料和功能梯度材料的设定。借助于这些功能,用户可以轻松创建各种自定义材料,包括带有工程属性的超材料、旋磁和旋波材料等。
通过直接在软件中修改材料、控制麦克斯韦方程组或边界条件,用户可以实现对仿真分析的全面掌控。
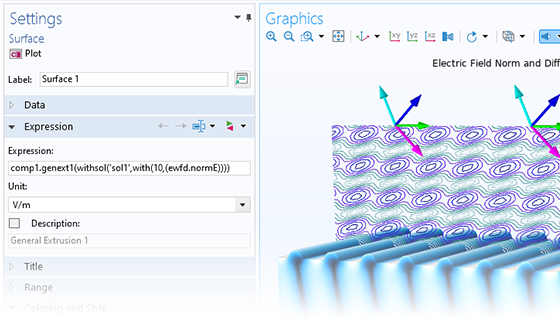
用户既可以通过各种绘图来直观地呈现电场和磁场、反射率、透光率、衍射效率、S 参数、功率流和耗散等计算结果,也可以对自定义的物理量进行可视化,以便更深入和全面地理解仿真结果。
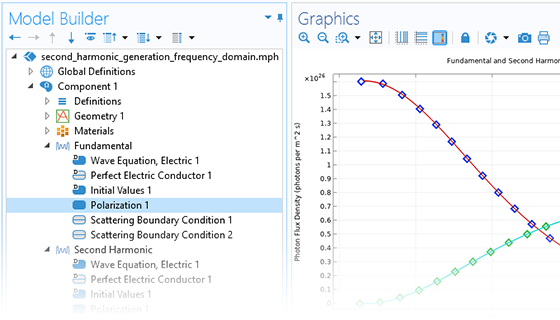
“波动光学模块”提供非线性光学问题的时域和频域仿真功能,支持对材料属性随温度或其他物理场变化的材料进行如自聚焦等非线性光学分析;支持耦合多个频域分析,来模拟不同频率下的两个或多个波之间的混合,如和频、差频产生过程。通过引入非线性偏振项,可以分析涉及连续波(CW)激光或其他准稳态现象的非线性光学仿真。时域分析的功能也非常灵活,用户可以修改偏振或残余电位移项,分析更复杂的建模场景,如皮秒、飞秒等超快激光现象。
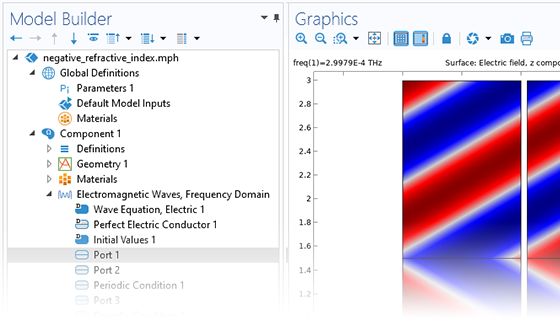
在电磁波建模中,准确的边界条件对于仿真结果的精度至关重要。“波动光学模块”提供专业的边界条件,可以处理光学仿真中的各种场景:支持无界域模拟;对于超材料等周期性结构,周期性端口可以处理任意入射角和衍射级;对于波导和光纤问题,模块提供模式匹配端口以确保正确地将入射光馈送入波导。
“波动光学模块”提供以下重要的边界条件:
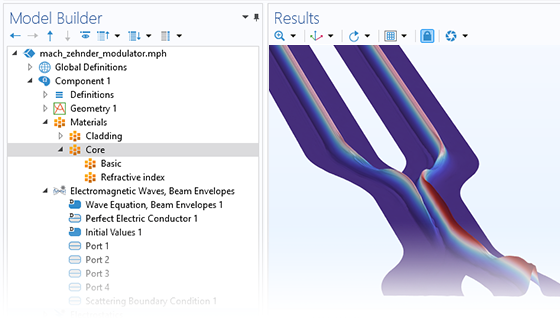
“波动光学模块”可与其他模块结合使用,以模拟光学器件中的多物理场现象,所有附加模块都与 COMSOL Multiphysics® 软件平台无缝集成。这意味着,不论研究哪种工程领域或物理现象,都可以遵循相同的仿真工作流程。
借助“波动光学模块”,用户可以研究机械变形对光学器件性能的影响,如应力-光效应,也可以研究热、热应力和热耗散对器件性能的影响;还可以分析如声光、电光和磁光效应等多种物理效应,并将结果用于光学调制。
与质量传递分析相耦合时,用户可以计算具有各向异性扩散系数的真实折射率曲线,并将结果用于电磁学分析,以便更好地了解光学器件的行为,优化器件的设计和性能。
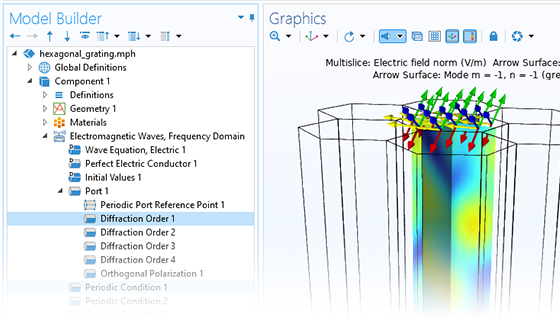
周期性结构是众多工程电磁结构的基础,广泛应用于偏振和亚波长成像以及衍射光学等领域。“波动光学模块”的 Floquet 周期条件和不同的衍射级可以用于分析这些结构(包括其高阶衍射模式),快速、准确地设计超表面和其他平面光学元件。
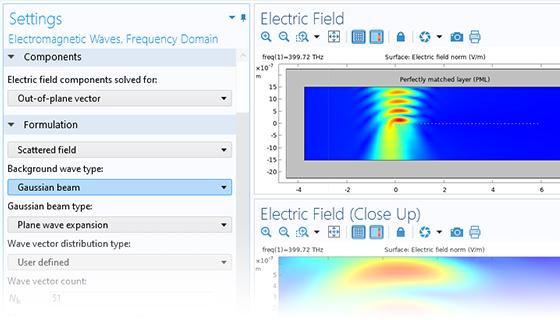
散射场公式可以用于轻松建立金纳米粒子等物体的精确散射模型:用户可以设置平面波、高斯光束(考虑或不考虑近轴近似)或自定义激励,对由激励引起的散射场进行求解;完美匹配层(PML)的出射辐射吸收功能,可以吸收各种频率和入射角范围内的辐射,用来近似无限大空间;近远场变换功能支持对散射体的远场辐射进行详细分析,从而更深入地了解散射现象。
COMSOL 是否能用于解决我的问题?
欢迎联系我们,我们的专业工程师可以协助您评估技术可行性,并根据使用场景推荐许可形式。
点击右侧的“联系 COMSOL”按钮,填写并提交信息,我们的工作人员将会尽快与您联系。
评估与试用 COMSOL® 软件