
本篇博客中,我们将简要介绍求解非线性稳态有限元问题的算法,并通过一个非常简单的一维有限元问题来演示这些内容,即我们在“求解线性稳态有限元模型”博客中所讨论的那个问题。
与刚性壁相连的弹簧系统
考虑下图所示的系统:弹簧的一端与刚性壁相连,对另一端施加应力。弹簧的刚度可表示为关于其拉伸距离的方程:k(u)=exp(u) ,即弹簧的刚度随弹簧拉伸呈指数增长。
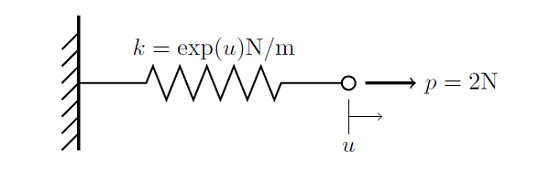
现需求出弹簧受力端的位移。与之前在线性 问题中的处理类似,我们可将描述非线性 有限元问题中某一节点受力平衡的方程写成如下形式:
在本案例中,只有弹簧的刚度和解有关;但在更多情况下,非线性问题中的载荷和单元的属性都可以任意依赖于解。
绘制上述方程,并请记住我们希望求出 使得 f(u)=0 的u。
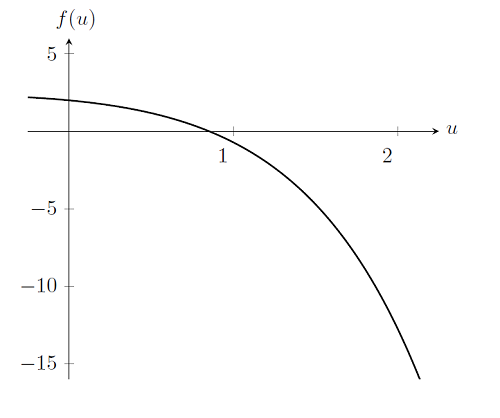
实际上,对这个问题的求解与线性问题只存在细微的差别。回想一下,在求解线性问题时我们使用了一次 Newton-Raphson 迭代——这里我们同样使用这种迭代方法:
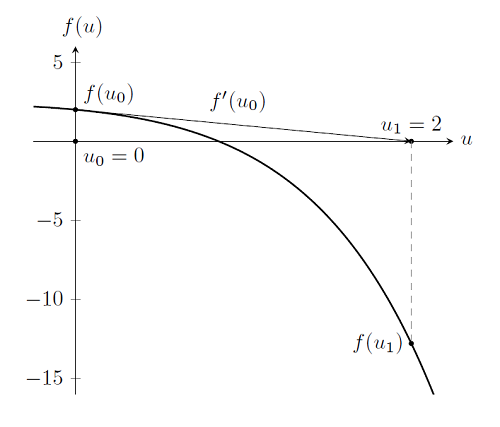
不难发现,我们又一次采取初始猜测:u_0=0 ,并计算方程 f(u_0),以及它的导数 f'(u_0)。 从而得到 u_1 。通过检验发现这不是解,因为 f(u_1) \ne 0。 但是如果继续使用 Newton-Raphson 迭代,很明显我们将会逐渐接近问题的解,如下图所示。(您可以点击 Newton-Raphson 迭代法来获取关于该算法的更多信息。)
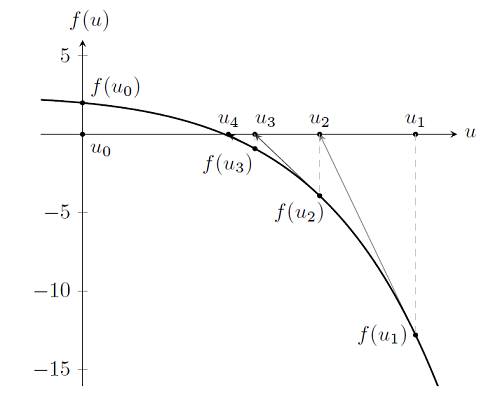
所以除了需要使用多次 Newton-Raphson 迭代求解,求解非线性问题和求解线性问题的本质相同,除了要使用多次 Newton-Raphson 迭代求解。实际上,我们可以继续使用迭代以任意接近真实解,但并没有必要这么做。之前也有讨论过,我们总是会碰到电脑数值精度的问题,所以只能达到一个接近真实解的实际极限。观察几次迭代后的结果:
| i | u_i | |f(u_i)| | |u_{i-1}-u_i| | |f(u_{i-1})-f(u_i)| |
|---|---|---|---|---|
| 0 | 0.000 | 2.000 | ||
| 1 | 2.000 | 12.77 | 2.000 | 10.77 |
| 2 | 1.424 | 3.915 | 0.576 | 8.855 |
| 3 | 1.035 | 0.914 | 0.389 | 3.001 |
| 4 | 0.876 | 0.104 | 0.159 | 0.810 |
| 5 | 0.853 | 0.002 | 0.023 | 0.102 |
| 6 | 0.852 | 0.001 | 0.001 | 0.001 |
经过六次迭代后我们发现 f(u) 和 u 的每两次之间的差值以 f(u) 的绝对值都减少到 0.001 甚至更小。经过从 u_0=0 开始的六次 Newton-Raphson 迭代后,解的误差收敛到 0.001 以内。当求解非线性问题时,我们都将使用这个算法直到解收敛至期望容差内。第二种终止准则:求解器不可以执行超过规定次数的迭代。无论哪种准则、容差还是迭代次数,只要满足一项后,求解器就将停止工作。同时应熟记“求解线性稳态有限元问题”博客中关于数值缩放问题的讨论。容差准则适用于缩放后的解矢量一而不是解的绝对值。
尽管对于求解当 u 为矢量时的情况进行绘制的难度更高,但使用的是相同的算法,即适用于典型非线性有限元问题。然而当求解涉及几百、几千甚至几百万自由度的问题时,执行 Newton-Raphson 迭代的次数越少越好。上文中提到需求解的等式:\mathbf{u}_{i+1}=\mathbf{u}_{i}-[\mathbf{f}'(\mathbf{u}_{i})]^{-1}\mathbf{f}(\mathbf{u}_{i}) ,且计算导函数的倒数是计算强度最高的步骤。 COMSOL 采用阻尼因子来避免运算至无解区域的情况,以及最小化 Newton-Raphson 迭代的次数。再考虑之前绘制的第一次 Newton-Raphson 迭代,并观察该步骤 |\mathbf{f}(\mathbf{u}_{i+1})|>|\mathbf{f}(\mathbf{u}_{i})| 。 所以对于该迭代取值过大。出现这类情况时, COMSOL 将会在 [\mathbf{u}_{i},\mathbf{u}_{i+1}] 区间上执行一个简单的搜索,并找到一点 \mathbf{u}_{damped}=\mathbf{u}_i+\alpha(\mathbf{u}_{i+1}-\mathbf{u}_i) 使得 |\mathbf{f(u}_{damped})|<|\mathbf{f(u}_{i})| 。然后在该点重新执行 Newton-Raphson 迭代。
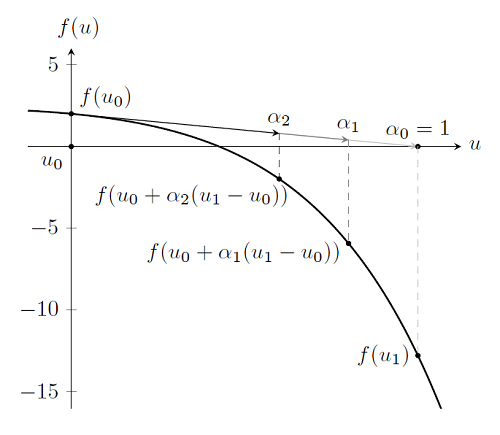
其中 \alpha 表示阻尼因子,且 0< \alpha \le 1 。 当 \alpha \rightarrow 0 即为阻尼 增加;当 \alpha = 1 时问题无阻尼。我们较喜欢采用这一方法,因为搜索过程仅需要 COMSOL 来计算 \mathbf{f(u}_{damped}) ,而且与计算导数 \mathbf{f'(u}_{i}) 和其倒数 [\mathbf{f}'(\mathbf{u}_i)]^\mathbf{-1} 相比,计算成本要低。
需要着重强调的是该阻尼项没有直接的物理解释。尽管这种算法能有效改善收敛,但是通过检验阻尼因子只能收集到极少量的物理信息。此外,尽管 COMSOL 允许您手动修改阻尼因子,但很难借助模型中的物理知识或信息来操作。我们通过人为干预计算得到的结果很难超过缺省的阻尼算法。不过,当缺省的阻尼 Newton-Raphson 方法收敛缓慢或完全不收敛时,还可以根据问题的物理场选择其他一些表现更为优异的技巧。
为什么非线性问题会不收敛
求解非线性问题向来较为困难,因为上述求解过程可能在许多情况下并不收敛。尽管 Newton-Raphson 方法失效的情况很多,但在实际操作中可以将不收敛归纳为以下几种情况:
情形 1 : 初始条件与解距离太远
首先考虑之前的非线性问题,但选择不同的起始点,例如 u_0=-2。 如下图所示,如果我们选择任意初始条件 u_0\le-1,那么使用 Newton-Raphson 法将无法求解,因为f(u) 的导数不指向解。 u_0=-1 的左侧区域无解,所以这些起始点在 Newton-Raphson 方法的收敛半径以外。即使存在解,对起始点的选择也可能造成 Newton-Raphson 方法无法收敛。所以与线性问题中一个被设定好的问题永远有解不同,非线性模型的收敛很大程度上依赖于初始条件的选择。我们会在后续博客中阐述如何选择合适的初始条件。
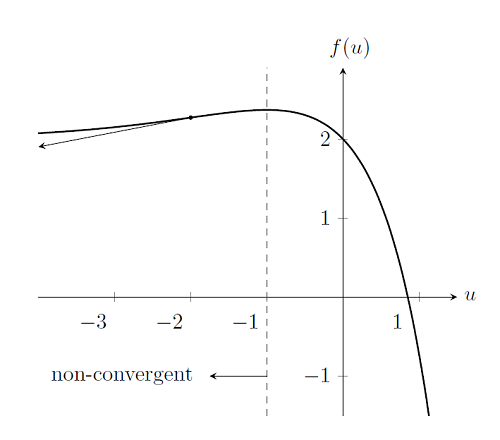
情形 2 : 问题无解
当问题本身无解时,非线性求解器也会失效。再次考虑上述问题,但是弹簧刚度为 k(u)=\exp(-u)。 即弹簧被拉伸时刚度减小。绘制出 p=2 时的 f(u)</span,可以看出问题无解。但 Newton-Raphson 法无法判断出该情况;算法将直接失效,并且在达到用户给出的迭代数后结束运算。
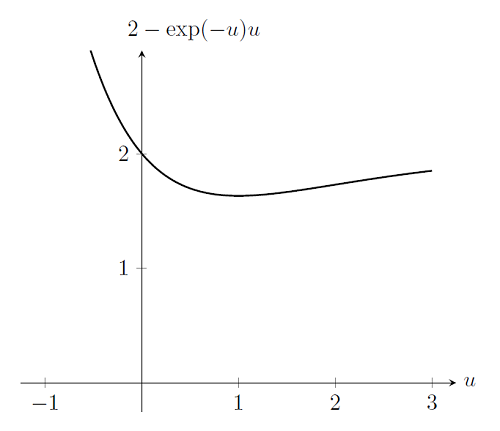
情形 3 : 问题不平滑且无法求导
最后考虑材料属性中存在不连续性的情况。譬如,仍然考虑上述问题,但是弹簧刚度在不同区间内有不同的值: u\le1.8 时 k=0.5,1.8<u<2.2 时 k=1 ,u\ge2.2 时 k=1.5。 如果绘制出相应的 f(u) 图像,可以发现是不可微且不连续,这就与 Newton-Raphson 方法需满足的条件相悖。通过检验可以很清楚地看出,除非选择 1.8<u<2.2 区间内的起始点,否则 Newton-Raphson 迭代会在区间外的迭代之间震荡。
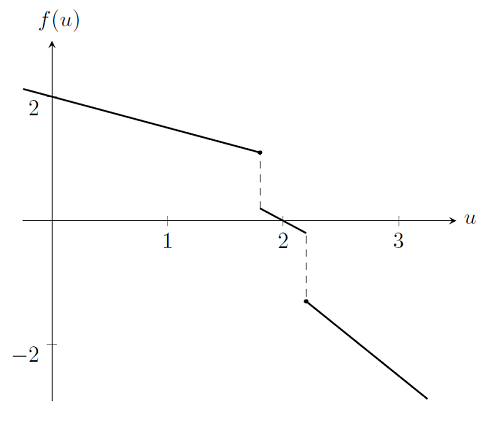
总结一下,截至目前我们已经介绍了使用阻尼 Newton-Raphson 法求解非线性有限元问题,并讨论了所使用的收敛准则。同时还介绍了几种算法失效的情况,包括:
- 选择的初始条件离解太远
- 设定的问题无解
- 定义的问题不平滑且不可微
读取 COMSOL 日志文件
日志文件
我们即将讨论阐述以上问题的几种方式,但是在此之前先来看一个代表性的非线性有限元问题的日志文件。以下是一个几何非线性结构力学问题的日志文件(已添加行号):
1) 求解器 1 稳态求解器 1开始于:10-Jul-2013 15:23:07. 2) 非线性求解器 3) 求解自由度数: 2002 。 4) 发现对称矩阵。 5) 因变量的缩放: 6) 位移场(材料) (mod1.u):1 7) 迭代数 ErrEst 阻尼 步长 #Res #Jac #Sol 8) 1 6.1 0.1112155 7 3 1 3 9) 2 0.12 0.6051934 1.2 4 2 5 10) 3 0.045 1.0000000 0.18 5 3 7 11) 4 0.012 1.0000000 0.075 6 4 9 12) 5 0.0012 1.0000000 0.018 7 5 11 13) 6 1.6e-005 1.0000000 0.0015 8 6 13 14) 求解器 1 稳态求解器 1 :求解时间: 1 s 15) 物理内存: 849 MB 16) 虚拟内存: 946 MB
注释
- 第 1 行报告了求解器的种类和开始时间。
- 第 2 行报告了软件正在下达指令给非线性系统求解器。
- 第 3 行以自由度数的形式报告了问题的大小。
- 第 4 行报告了待求有限元矩阵的种类。
- 第 5-6 行报告了缩放比例。在本案例中,位移场的尺寸是 1 m,对解的期望级数较为合适。
- 第 7-13 行报告了经过六次 Newton-Raphson 迭代后解收敛。第一列报告了迭代次数,第二列报告了定义收敛所采用的误差估计。收敛准则的缺省值为 0.001 。第三列显示了前两步中使用的阻尼,而第 3-6 步无阻尼。
- 第 14-16 行报告了求解时间和内存要求。
现在您应该已经了解 COMSOL 如何求解非线性稳态有限元问题,以及怎样读取日志文件。




评论 (0)