
你知道怎样找到湖上两点之间最短的陆路距离吗?这种障碍物和解的边界通常被称为不等式约束。在接触力学中对物体间隙非负性的要求,在化学中对物种浓度的要求,以及在生态学中对种群的要求都是不平等约束的一些例子。在之前的系列博客中,我们讨论了变分问题中的等式约束。今天,我们将向您介绍如何在 COMSOL Multiphysics® 中基于方程建模时实现不等式约束。
用于路径规划的罚函数法
假设你想从(0,0.2)点移动到(1,1)点,但是有一个圆心在(0.5,0.5),半径为 0.2 的圆形障碍物。使两个端点 (a,u(a)) 和 (b,u(b)) 之间的距离最小的曲线 (x,u) 应该使函数最小
在欧几里得空间中,两点之间最短的距离是直线。因此,用我们已经讨论过的方法来解这个方程应该会得到一条直线。然而,在我们的例子中,这条直线穿过了障碍物。这是不可行的。我们必须遵循我们的路径不能进入障碍物的约束;即路径上某一点到圆形障碍物中心的距离应该大于或等于圆的半径。
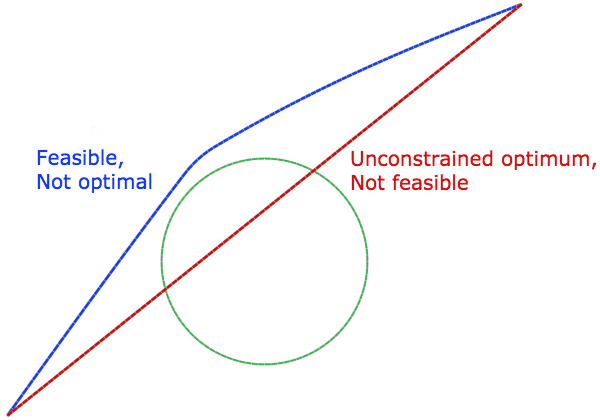
不等式约束问题的一个基本示意图。
我们要在函数中添加一个术语来惩罚约束违背。对于等式约束 g=0,我们惩罚 g 的正负值。对于不等式约束 g \leq 0,我们惩罚 g 的正值,而接受负值。
在障碍物问题中,这意味着只有当路径试图穿过障碍时,我们才能进行惩罚。远离环形湖的海岸是可行的,虽然可能不是最优的,因此我们的惩罚正则化目标函数是
^2}dx + \frac{\mu}{2}\int_a^b\bigg\langle R-\sqrt{(x-x_o)^2+(u(x)-y_o)^2}\bigg\rangle^2dx,
其中,\mu 是惩罚参数,我们使用斜坡函数
x& x\ge 00 & x \le 0.\end{cases}
对于一般函数
在不等式约束下被最小化
惩罚函数变成
最后一步是对上述函数求一阶变分导数,并将其设为零。这里,我们需要记住斜坡函数的导数是 Heaviside 阶跃函数 H。
在上面的推导中,我们使用了 \big \langle x \big \rangle H _x= xH_x. 这一事实。注意,我们在这里讨论的是非正性约束。非负性约束可以通过取约束方程的负,求解等价的非正性约束来处理。
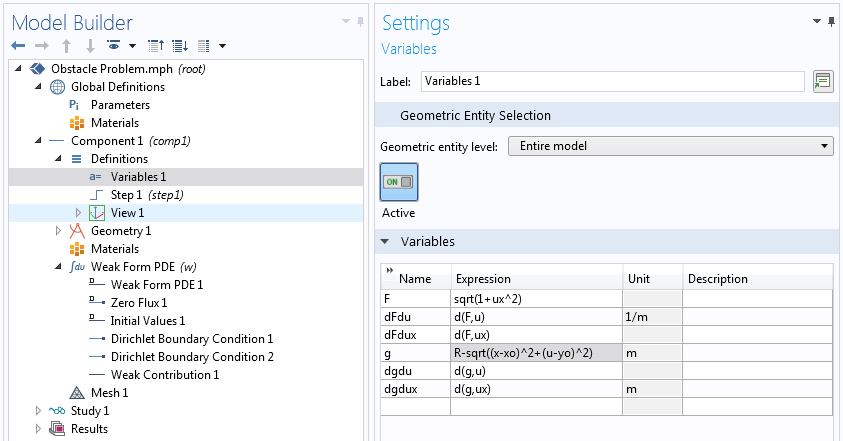
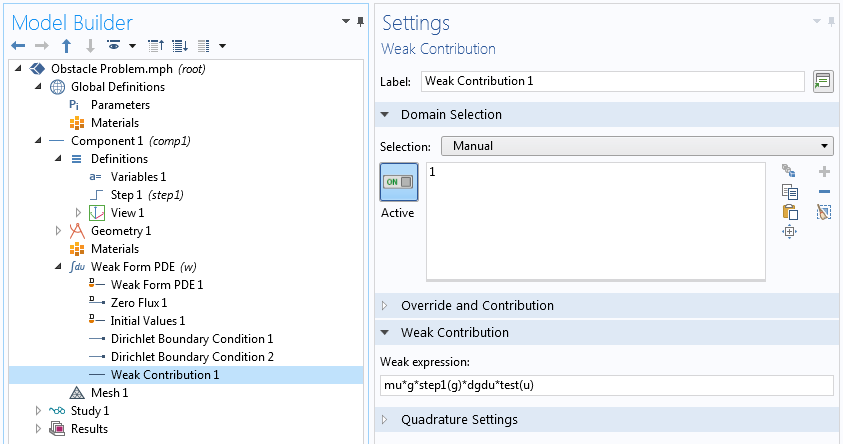
上面变分方程的第一项是来自无约束问题的似曾相识的贡献。让我们看看如何使用 COMSOL 中的弱贡献节点添加惩罚项。我们将使用更简单的狄利克雷边界条件 节点来固定端点。
用罚函数法实现不等式约束。
注意,在上面的弱贡献中,我们没有包含 \frac{\partial g}
{\partial u^{\prime}},因为这个问题的约束只依赖于解,而不依赖于它的空间导数。
对一个递增的罚参数序列求解这个问题,同时重新利用前面的解作为初始估计,我们得到如下结果。
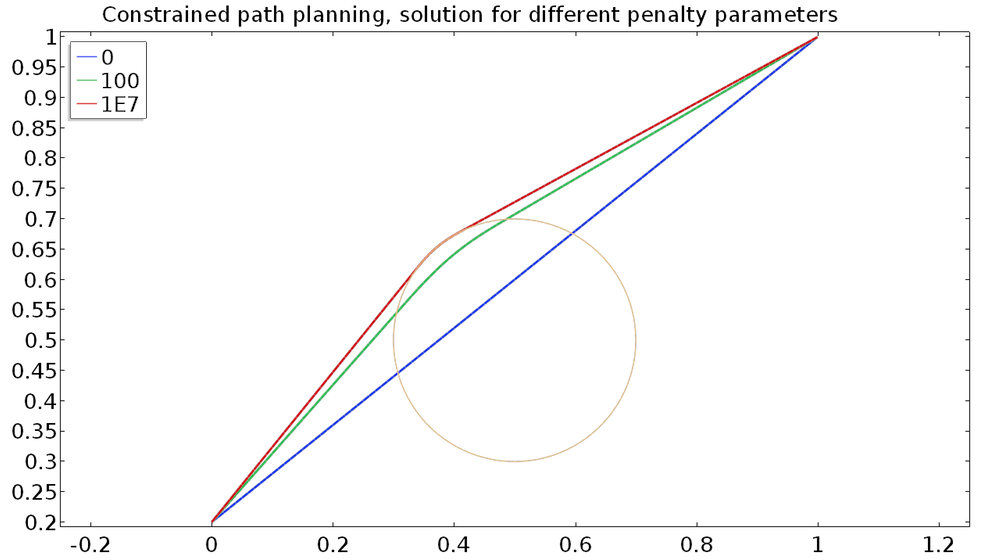
使用罚函数法寻找绕过障碍物的最短路径。零惩罚返回无约束解。
在讨论等式约束罚函数法的物理解释时,我们已经说过罚项引入了一个与违反约束成比例的反应。这种解释适用,但对于不平等约束,反应是片面的。
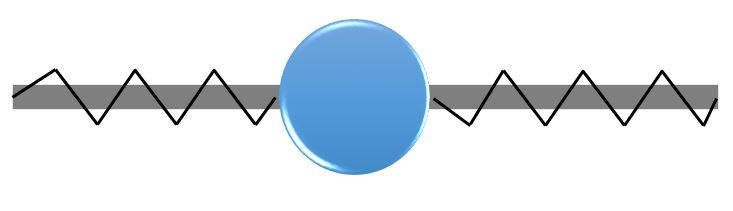
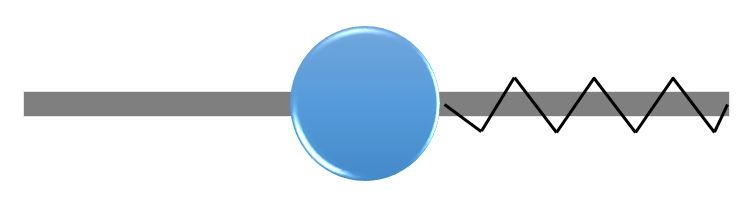
想象一下,使用压缩弹簧迫使一颗珠子留在原地。弹簧没有钩在珠上;他们只是接触。为了使珠子保持在x=0,我们必须在原点的每一边使用一个弹簧。如果珠子到原点的左边是可以接受的,那我们的约束是 ,我们必须只有右侧存在把压缩弹簧。这就是为什么我们惩罚是 \big \langle g \big \rangle 而不是 |g|。
一个弹簧的罚函数执行平等(多边)和不平等(单边)约束。
拉格朗日乘子法
在讨论不同约束执行策略的数值性质时,我们讨论过虽然拉格朗日乘子法严格执行约束,但它在数值解中有一些不受欢迎的性质。也就是说,它对解的初始估计很敏感,可能需要直接线性求解器。这些不利因素仍然存在,但在不平等限制下,还有一个额外的挑战。具体来说,就是约束可能并不总是活跃的。
考虑我们的路径规划问题。在不接触障碍物的部分路径中,约束是未激活的。然而,我们事先不知道哪些约束是有效的,哪些是无效的。有几种策略可以解决这个问题,下面我们只介绍两种常用的方法。
有效集策略
假设有些约束是有效的,有些不是。在一个分布式约束中,这意味着选择 g=0 的点,并假设其他点在 g <0. 的可行区域内。在不活跃点,拉格朗日乘数应为零。在有效集上,拉格朗日乘数不应为负。这就是所谓的 Karush-Kuhn-Tucker (KKT) 条件。如果在计算后,有效集发生了变化或违反了 KKT 条件,我们必须适当地更新有效集并重新计算。下面的流程图总结了这一过程:
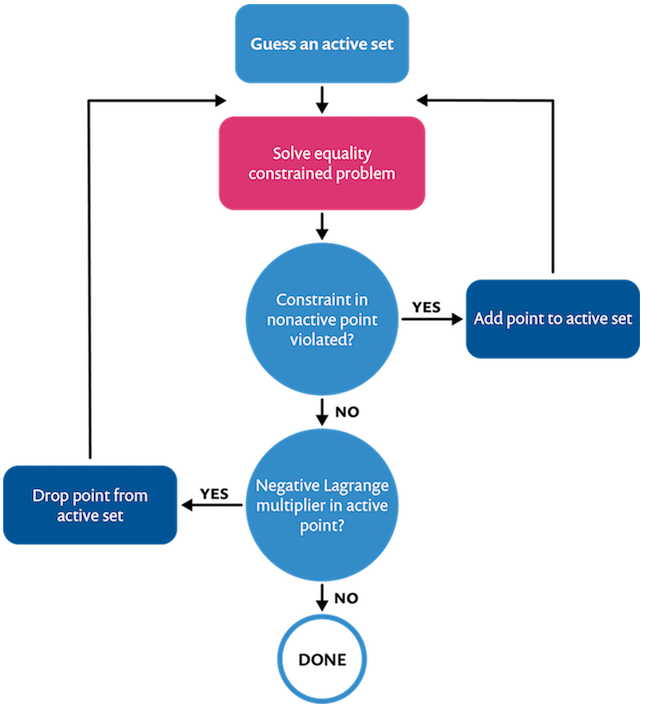
不等式约束的拉格朗日乘子执行的有效集策略。
通过这个迭代过程,每次迭代求解一个等式约束问题。等式约束的拉格朗日乘子实施已经在本系列的前一篇博文中讨论过了。
松弛变量
约束 g \leq 0 相当于 g + s^2=0。现在我们有一个引入新松弛变量的等式约束。如果不等式是分布式(逐点)约束,则松弛变量以及拉格朗日乘数都是函数。
一方面,松弛变量策略引入了另一个未知待解,但却一举解决了问题。另一方面,有效集策略不需要这个变量,但必须解决多个问题,直到有效集停止变化。
增广拉格朗日方法
就像我们处理等式约束一样,我们可以用一个微积分问题来讨论这个方法的基本思想。用拉格朗日乘数项、估计乘数项和惩罚项对无约束目标函数进行增广,得到
{\mu} {2}\big\langle g\big \rangle^2.
这个约束条件的一阶最优条件为
= 0.
这意味着乘数更新
如果我们从对拉格朗日乘数的初始估计为零开始,那么上述等式仅在以下情况更新拉格朗日乘数 是有效的。因此,拉格朗日乘数永远不会为负,并且仅在倾向于违反约束的点上为正。
增广拉格朗日方法是一种近似约束强制策略,将允许对约束的轻微违反。事实上,如果没有违反约束,拉格朗日乘数保持为零。因此,该策略完全满足 KKT 条件的双重可行性部分(\lambda \ge 0),但仅近似满足互补松弛部分 (\lambda g = 0)。拉格朗日乘数法完全满足这两个条件。
不规则形状的障碍物
在今天的例子中,我们使用了一个非常理想化的湖泊,它的边界可以用一个简单的函数来描述。也可能是一个水池。有时,不等式约束有这样简单的解析形式。化学反应或种群动力学中的非负性约束就是这方面的例子。然而,其他约束没有这样简单的形式。
例如,在接触力学中,我们希望保持接触物体之间的间隙为非负值,但物体的边界很少如此简单,因此我们可以用平滑的解析函数来定义它们。最重要的是,对于大变形问题,我们希望在变形域上强制接触约束,但我们肯定没有对变形域的解析描述。因此,约束必须从满足离散版本的对象的网格下获得。当物体移动和变形时,必须使用复杂的搜索操作来找出哪些点与其他点接触或不接触。在 COMSOL Multiphysics® 软件中有用于这个和其他接触仿真程序的内置功能。
对于一些简单的几何形状和变形,我们可以使用广义拉伸算子来计算变形对象之间的距离,而无需使用接触力学功能。更复杂的几何图形才需要后者。
下一步
到目前为止,在本系列博客中,我们已经介绍了如何使用 COMSOL Multiphysics 解决有约束和无约束变分问题,并讨论了实施约束的不同数值策略的优缺点。也就是说,我们仅限于一维单物理场问题和变分问题,最多只有泛函中的一阶导数。
有了这个主题的基础知识,希望我们已经准备好处理高维数、高阶导数和多种领域的应用。这将在本系列的下一篇也是最后一篇博文中介绍。请继续关注!
查看更多关于变分问题和约束系列的博客文章
- 第1部分:肥皂膜和其他变分问题建模概述
- 第2部分:在变分问题中指定边界条件和约束
- 第3部分:强制约束中数值问题的处理方法
- 第5部分:图像去噪以及其他多维变分问题



评论 (2)
yi chen
2021-11-08请问一下,这篇博客的案例可以提供一下吗?
hao huang
2021-11-08 COMSOL 员工您好,抱歉该博客暂时还没有相关案例。