
在有限元建模中,你可能会遇到力不随位移单调递增的计算公式。我们可以在许多包括材料退化的材料模型中看到这种特性。这种行为可以用负刚度来表示。在这篇博客中,我们讨论了负刚度的一些例子,包括它所代表的物理背景和数值意义。这些想法并不局限于力学分析,虽然刚度起源于该领域。
关于负刚度的一个例子
考虑一个承受了压缩载荷的对称两杆结构,如下图所示。
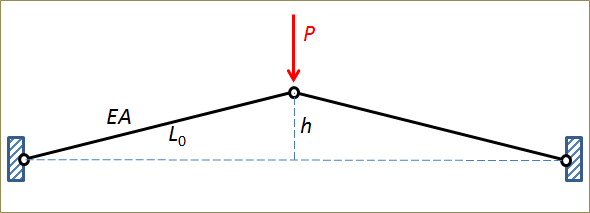
承受了压缩载荷的两杆。
假设杆是线性弹性的,所以杆中的力 F,可以表示为
式中,Δ 是伸长率, L0 是杆的原始长度。
根据毕达哥拉斯定理(Pythagoras’ theorem),我们可以将垂直力写成垂直位移的明确函数。
-1 \right) \frac{\kappa(1-\delta)}{\sqrt{1+\kappa^2\delta(\delta-2)}} \approx EA \kappa^3\delta(\delta-2)(\delta-1)
式中的一些量做了无量纲化处理:
- 归一化的位移 \delta = w/h,其中 w 是负载下的挠度。因此,当杆处于水平时 \delta = 1,当结构倒置时 \delta = 2。
- 参数 \kappa = h/L_0 是杆的初始高度与初始长度之比。
力与位移的函数如下图所示。这个例子实际上显示的是一个包含突弹跳变的屈曲问题。在点 A 和点 C 之间,不存在唯一的解。在之前的一篇博客中,我们深入讨论了结构中屈曲的概念。
杆件的压缩力增加,直到它们处于水平时(\delta=1),但垂直投影在 A 点之后下降得更快。
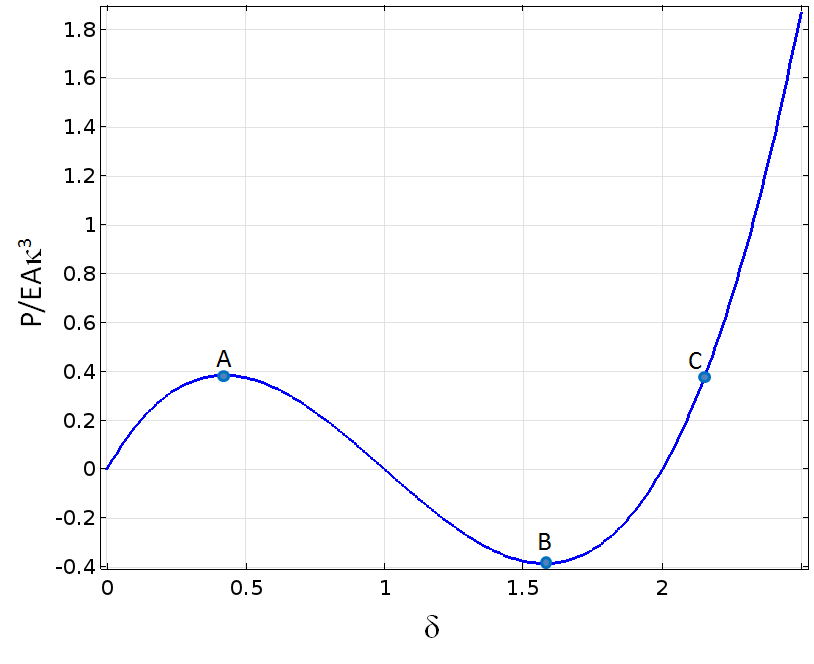
力是垂直位移的一个函数。
如果我们为这个结构建立一个有限元模型,并尝试增加载荷,那么当在A点达到第一个峰值时,分析可能会失败。但是,我们可以通过指定载荷点的垂直位移,而不是力来轻松完成解的追踪。那么,施加的力就可以作为反作用力得到。上图就是用这种方法制作的。
这个单自由度系统的切向刚度被定义为力相对于位移的变化率。
因此,在 A 点和 B 点之间的刚度是负的。负刚度通常与数值和物理不稳定性有关。
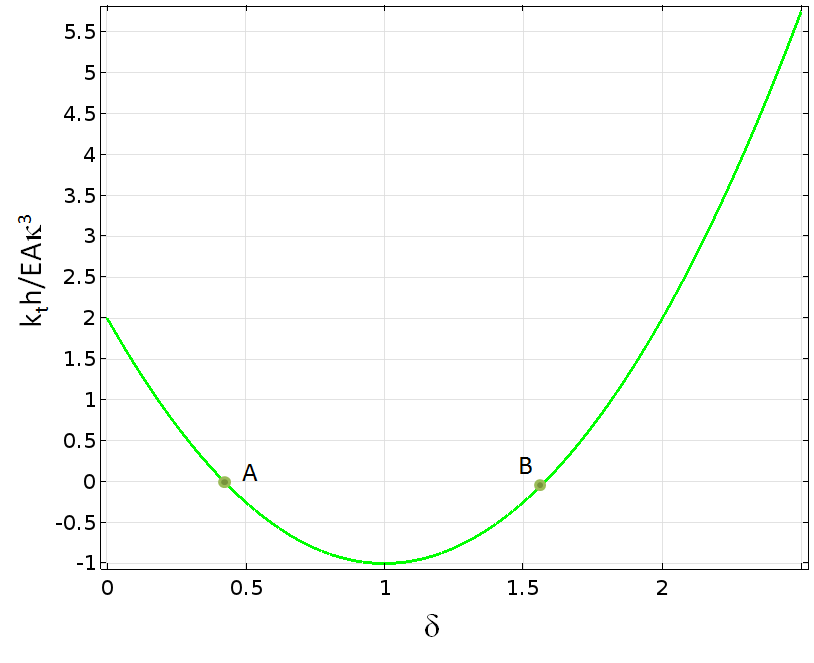
刚度是垂直位移的函数。
软化材料中的负刚度
在固体力学领域,有几个材料模型包含了应力-应变曲线的负斜率,有的是有意为之,有的是在选择某些参数的情况下产生的。例如,一些混凝土的模型就是这样设计的。对这种行为的物理解释是,当材料模型被拉伸时,会形成裂缝。然后,测试样本所承载的载荷将减少。COMSOL Multiphysics® 软件中用于描述剥离的内聚力模型也显示了这种行为。
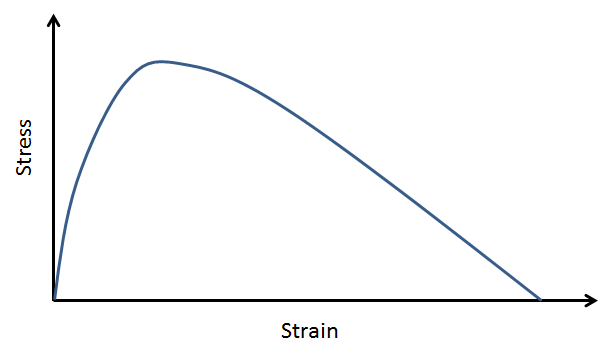
一种应变软化材料
在材料层面,随着应变的增加,应力不断减小,表明刚度是负的。
这样的材料只能在指定位移条件下进行测试;否则,当达到峰值载荷时,它将立即失效。因此,负刚度与材料的不稳定性有关。
一般来说,应力和应变状态是多轴的。应力和应变是由二阶张量表示的。在多轴情况下,我们必须使用一个更普遍的材料稳定性标准。对于应变状态的任何微小变化,应力状态的相应变化必须使所有应力和应变分量的乘积之和为正。也就是说
或者,以分量的形式写出来。
这被称为德鲁克稳定性标准(Drucker’s stability criterion)或希尔稳定性标准(Hill’s stability criterion)。
在有限元分析中使用的离散形式意味着,与应力增量和应变增量相关的本构矩阵必须是正定的,以使材料是稳定的。对于非线性材料来说,这个条件通常在计算上代价较高。对于线性弹性材料,该要求可以直接转化为众所周知的 E>0 和 \quad -1< \nu < 0.5。
我们有时需要使用不符合稳定性标准的材料模型,该如何处理?事实上,材料可能是局部不稳定的,而结构本身仍然是稳定的。
为了理解这种行为,我们可以把结构中的材料想象成连接的弹簧。有些弹簧是纯弹性的,代表未损坏的材料,其中的某一个弹簧会失效。考虑下图中的三弹簧系统。
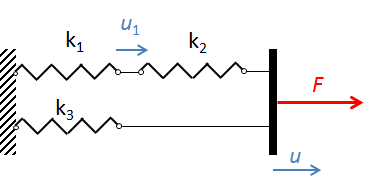
三弹簧系统。失效弹簧的伸长用 u1 表示。
弹簧 k1 代表具有损伤模型的材料,而其他两个弹簧是纯弹性的。第一个弹簧的材料模型是双线性的。
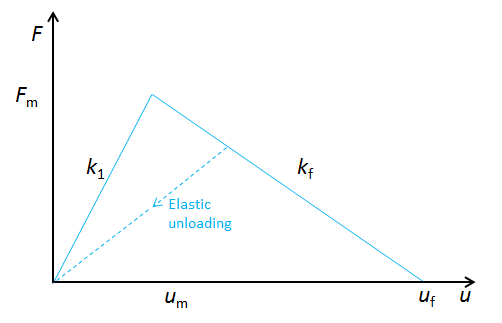
非线性弹簧的材料模型。在位移 um 处达到力的峰值 Fm。
下部分支的力与损伤无关:
因为两个弹簧是串联在一起的,所以在达到峰值负荷之前,上部分支的力
当上部分支的力为 F_u = F_m 时,损坏开始;也就是说当外部位移为:
相应的外力是
在失效过程中,受损弹簧的力可以写成 F_u = F_m-k_f \left(u_1-u_m \right)。同样的力也通过弹簧 2,所以 F_u = k_2(u-u_1)。
这两个关系决定了 u1 是外部位移的一个函数:
为了给出一个合理的解决方案,当外部位移增加时,u1 必须增加。因此,必须使 k_2 > k_f。这种迹象其实是非常普遍的结果。力(或应力)的快速下降比缓慢下降更容易导致不稳定。
最后,我们可以推导出下降阶段的总外力和位移之间的关系:
因此,当外部位移增加时,外力可以增加或减少,这取决于两个分支的相对刚度。这个简单的模型因此可以预测两种类型的不稳定性。
- 如果 k_2 > k_f,上部分支变得不稳定,
- 如果 k_3 < \frac{k_2k_f}{k_2-k_f} 总的系统也不稳定,即使 k_2 < k_f
在这两种情况下,损伤模型中的力的缓慢下降是有益的。换句话说,周围环境越刚性,整个系统就越有可能稳定。
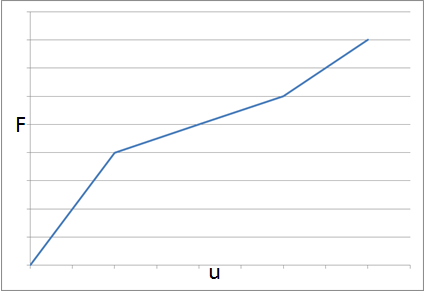
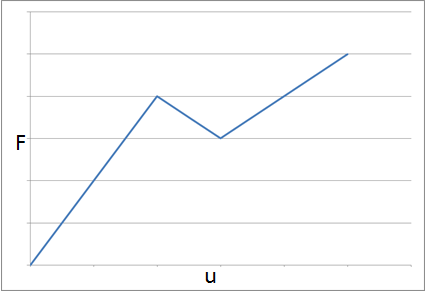
一个全局稳定的系统(左)和一个因下部分支的刚度太小而无法维持稳定的系统(右)。
在现实中,我们不能自由选择力和刚度。材料模型中的三角形力-位移曲线下的面积代表过程中耗散的能量。能量耗散和最终失效时的位移(或应变)具有物理意义。
能量平衡的解释
当承受的力减少时,结构的损坏部分会伸长。如果外部位移保持固定,那么结构的弹性部分必须收缩以进行补偿。这意味着弹性能量被释放。吸收能量的唯一方法是对受损部分做功。对于一定的增量位移 \Delta u_1,如果弹性部分释放的能量大于在纹裂部分产生相同位移所需的功,那么这个状态是不稳定的。
几年前,我在斯德哥尔摩 KTH 皇家理工学院固体力学系的一个朋友做了一些有趣的实验,他用极长的三点弯曲测试试样研究了韧性钢中裂纹的稳定性。这些试验强调,裂纹稳定性不仅是局部应力状态的函数,也是测试试样中存储的能量驱动裂纹伸长的能力。实验中最长的测试试样有 26 米,占据了实验室的很大一部分空间! 这个实验被发表在 International Journal of Pressure Vessels and Piping 中的文章“The stability of very long bend specimens” 里。
均质应力状态
对于软化材料模型,如果应力状态是均匀的,在有限元模型中实现收敛是非常困难的。
在物理材料中,强度并不具有完全均匀的分布。当增加载荷后,即使应力状态是均匀的,也会在强度最低的位置形成裂缝。当发生这种情况时,周围的材料就会失去载荷。
以下面这个由两个胶水层连接的三个弹性块为例来说明:

在现实中,其中一个胶水层会比另一个胶水层先失效。当通过组件的力减少时,稍强的那层将被卸下。我们无法预测哪一层会失效,因为这是由制造的不精确性控制的。然而,在数学模型中,两层会同时失效。在数值上,迭代可能不会收敛,因为疲劳在两层之间来回跳动。
在有限元模型中,应力是在每个单元内的每个积分点计算的。当载荷增加到最大值以上时,疲劳甚至可能在单元之间或同一单元内的各个积分点之间跳跃(如果各处的应力相同)。
这种行为意味着,如果我们实现自己的包含应变软化的材料模型,应该使用单一的一阶单元并在指定位移下测试它。这样一来,我们就能确保一个均匀的指定应变场,而且单元中各处的应力都是一样的。Mazar 的损伤模型就是这样一个例子,我们在以前的博客中介绍过。如果我们将该模型中的单元形状函数改为二次函数,计算将不再收敛。
这是否意味着损伤模型毫无意义?完全不是。然而,我们必须注意避免不确定的状态。如果一个结构和它的边界条件是对称的,为了避免不确定状态,必须采用这种对称性。我们通常可以通过使用轴向对称的模型来解决轴向对称的问题,而使用三维实体扇形的模型则可能不行。另一种方法是允许材料数据有轻微的随机空间扰动。这种方法实际上模仿了自然界,其中的强度值是随机分布的。另外,为了避免大部分的结构同时切换到失效状态,缓慢增加载荷是很重要的。
剪切带
在一些材料模型中,例如,在塑性土壤内,会出现具有高剪切应变的强网格依赖薄层。这些层被称为剪切带。当屈服刚开始时,周围的单元甚至积分点都是没有载荷的。第一个屈服的单元继续积累塑性应变。有趣的是,这种类型的不稳定性实际上可以在真实的土壤中看到,而不仅仅是数值模型中的一个假象。就像在自然界一样,我们无法预测模型中剪切带的确切位置和分布。
克服 COMSOL Multiphysics® 中的不稳定性
正如在文章开头的例子中提到的,使用指定位移而不是指定力是稳定数值问题的一个好方法。然而,这种方法基本上只限于以下情况:
- 单点载荷可以用指定位移代替。
- 应变状态是均匀的,例如在进行材料模型的单元测试时,因此位移在整个边界上是相同的。
- 不稳定性可以由外部边界条件控制。在上面讨论的弹簧装置中,由于 k3 值太小而引起的全局不稳定可以通过使用指定位移来固化,但在上层分支内的不稳定则不能固化。
我们可以采用一种更普遍的方法来解决过了不稳定点的问题。在这种方法中,首先定义一个已知单调递增的任意量,然后增加一个额外的方程,求解指定载荷或位移的相应值。
为了演示这种技术,(让我们在最初的例子中增加一个弹簧),这样就可以通过指定弹簧末端的变形来施加载荷。如果弹簧非常坚硬,这基本上与直接指定位移是一样的。
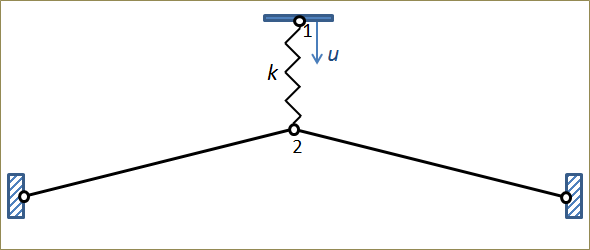
通过弹簧加载的杆系统。
如果弹簧比较软,系统可能会变得不稳定,因为弹簧可以释放出太多的能量。临界值是
这是杆组件的最大“负刚度”,当杆处于水平状态时,会出现这种情况。当改变弹簧刚度时,点 1 的力和位移之间的关系如下所示。弹簧刚度的公式为
其中系数 β 从一个基本刚性的弹簧变化到低于临界值的数值。
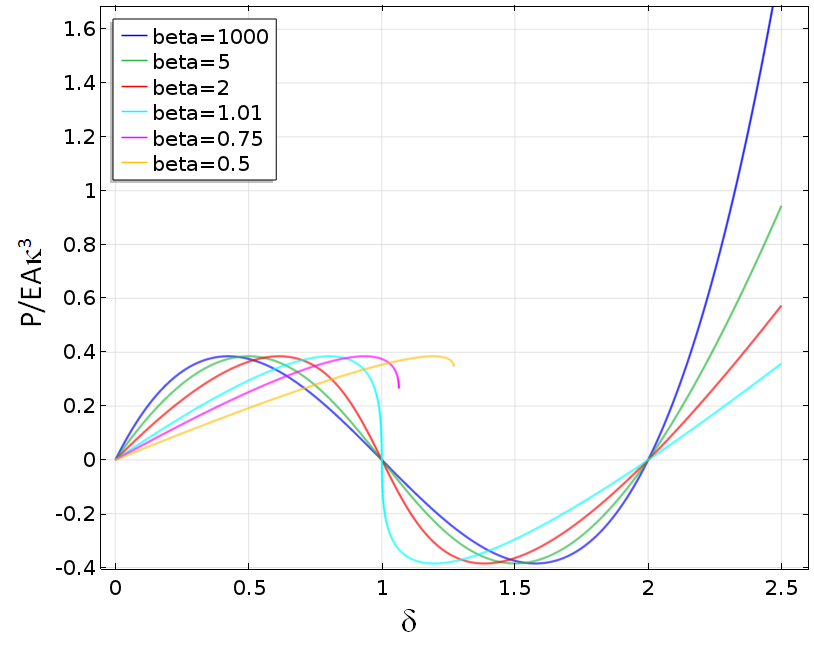
改变弹簧刚度时,力是点 1 位移的函数。
对于 β 小于 1 的值,当弹簧刚度等于杆组件的”负”刚度时,解失效。
如果用指定的力来代替,所有的解都会在第一个峰值载荷时失效。通过使用指定的位移,有可能继续进行进一步的分析。对于较低的弹簧刚度值,我们仍然受到内部不稳定导致失效时的状态的限制。
我们想追踪的解在点 2 有一个单调的垂直位移,但直接指定它是不可能的,因为这将从根本上改变问题。相反,我们添加了一个方程,并说明”设置点 1 的弹簧末端位移,使点2的监测位移具有指定的值。” 要做到这一点,需要添加一个全局方程 节点,在其中添加一个新的未知变量 disp_at_P1。
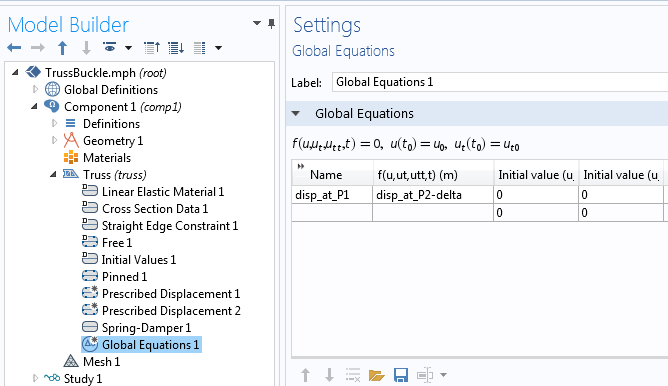
全局变量的定义
确定 disp_at_P1 值的方程指出, disp_at_P2-delta = 0。变量 delta 是在稳态研究步骤中递增的单调参数, disp_at_P2 是一个变量,包含点 2 的位移的当前值。
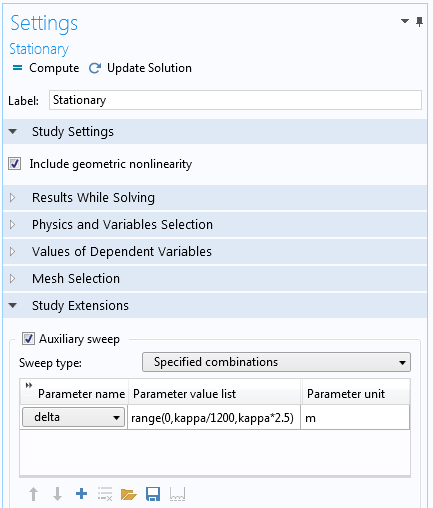
研究步骤的设置,其中 delta 被用作辅助扫频参数。
求解后,点 2 的位移将与辅助扫频中指定的 delta 值列表相匹配。
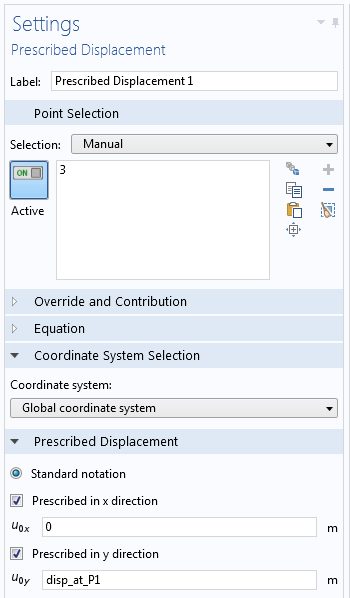
在点 1 的指定位移的设置。
通过这种修改,有可能通过不稳定性追踪解。从下图可以看出,使用这种方法甚至可以绕过强不稳定性。
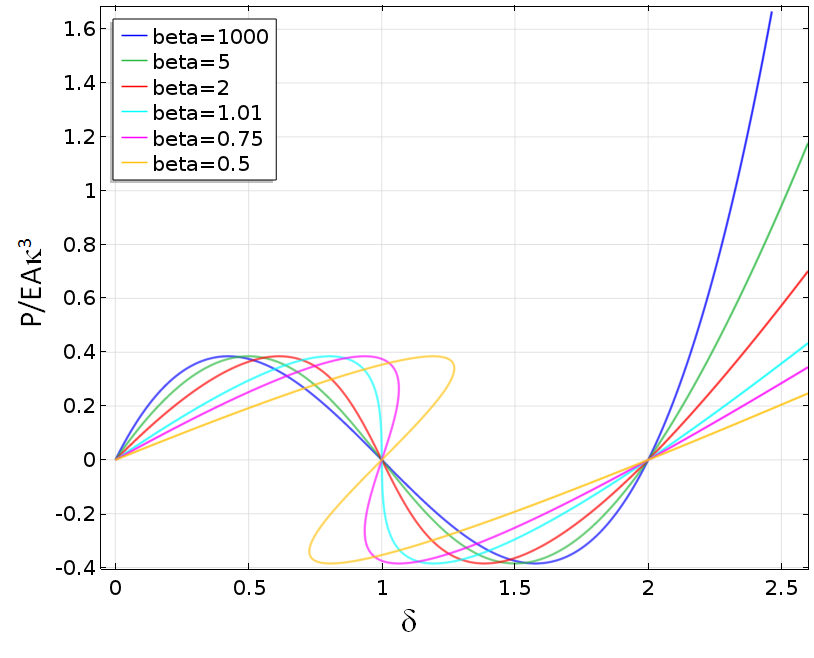
用 全局方程节点稳定后,改变弹簧刚度时,力是点 1 位移的函数。
拓展阅读
- 欢迎浏览 COMSOL 官网的“案例下载”页面中的其他案例,了解更多关于结构中负刚度和不稳定性模拟的应用。
- Kaiser, “The stability of very long bend specimens”, Int. J. Pres. Ves, & Piping.17 (1984) 1–17.





评论 (0)